| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 자유 프로젝트
- MapSqlParameterSource
- 코드스쿼드max
- NamedParameterJdbcTemplate
- 채팅목록조회
- Map.of()
- JazzMeet
- Til
- 재즈밋
- Python
- 실패했지만성공했다
- 백준
- 회고
- 3주차 회고
- Spring
- 파이썬
- Paths.get()
- 코드스쿼드
- BOJ
- 누구나 자료구조와 알고리즘
- requested
- 231103
- MAX
- 2023
- 22년도
- new File().toPath()
- rotuter
- baeldung
- 오류
- 테이크스트라
- Today
- Total
어제보다 한걸음 더
[책] 누구나 자료구조와 알고리즘 - 13장 속도를 높이는 재귀 알고리즘 본문
https://product.kyobobook.co.kr/detail/S000001834743
누구나 자료 구조와 알고리즘 | 제이 웬그로우 - 교보문고
누구나 자료 구조와 알고리즘 | 사칙 연산으로 복잡한 알고리즘을 쉽게 이해해보자 수학 용어와 전문 용어가 아니어도 이해한다 이 분야의 책은 대부분 컴퓨터 공학 전공자를 대상으로 쓰였거
product.kyobobook.co.kr
퀵정렬(Quicksort)은 컴퓨터 언어 중 대다수가 내부적으로 채택한 정렬 알고리즘이다.
재귀를 사용함에도 불구하고 어떻게 알고리즘의 속도를 크게 향상시키는지 배우고, 실제 쓰이고 있는 다른 실용적인 알고리즘에도 똑같이 적용해볼 수 있다.
퀵정렬은 매우 빠른 정렬 알고리즘으로 특히 평균 시나리오에서 효율적이다.
최악의 시나리오(역순으로 정렬된 배열)에서는 삽입 정렬이나 선택 정렬과 성능이 유사하지만 대부분의 경우 일어나는 평균 시나리오에서는 훨씬 빠르다.
퀵 정렬은 분할(partitioning)이라는 개념에 기반하므로 분할을 먼저 알아본다.
분할
배열을 분할(partition) 한다는 것은 배열로부터 임의의 수를 정해 피벗(pivot)이라 부르고 피벗보다 작은 수는 피벗의 왼쪽에, 피벗보다 큰 모든 수는 피벗의 오른쪽에 두는 것이다.
[0, 5, 2, 1, 6, 3] 의 배열이 있다.
- 임의의 피벗을 고른다. 여기서는 오른쪽 끝의 3을 피벗으로 선택했다. (중앙이나 왼쪽 끝의 값을 선택해도 된다.)
- 왼쪽 포인터는 0부터 시작한다. 3보다 큰 수를 만나거나 배열 끝에 도달하면 멈춘다.
- 오른쪽 포인터는 6부터 시작한다. 배열의 시작에 도달하면 멈춘다.
- 왼쪽 포인터와 오른쪽 포인터가 멈춰 있을 때, 가리키고 있는 값을 서로 교환한다. (1, 2, 3, 4단계를 반복한다.)
- 단, 왼쪽 포인터와 오른쪽 포인터가 같은 위치에서 만나면 멈추고, 가리키고 있는 값과 3(피벗)을 바꾼다.
다음과 같은 절차로 진행된다.





이 과정을 거치면 임시 정렬된 상태가 된다.
코드 구현: 분할
# 루비로 작성된 코드
class SortableArray
attr_reader :array
def initialize(array)
@array = array
end
def partition!(left_pointer, right_pointer)
# 항상 가장 오른쪽에 있는 값을 피벗으로 선택한다.
# 나중에 사용할 수 있도록 피벗의 인덱스를 저장한다.
pivot_index = right_pointer
# 피벗의 값을 저장해둔다.
pivot = @array[pivot_index]
# 피벗 바로 왼쪽에서 오른쪽 포인터를 시작시킨다.
right_pointer -= 1
while true do
# 피벗보다 크거나 같은 값을 가리킬 때까지
# 왼쪽 포인터를 오른쪽으로 옮긴다.
while @array[left_pointer] < pivot do
left_pointer += 1
end
# 피벗보다 작거나 같은 값을 가리킬 때까지
# 오른쪽 포인터를 왼쪽으로 옮긴다.
while @array[right_pointer] > pivot do
right_pointer -= 1
end
# 이제 왼쪽 초인터와 오른쪽 포인터 모두 이동을 멈췄다.
# 왼쪽 포인터가 오른쪽 포인터에 도달했거나 넘어섰는지 확인한다.
# 그렇다면 루프를 빠져 나가 이후에 코드에서 피벗을 교환한다.
if left_pointer >= right_pointer
break
# 왼쪽 포인터가 오른쪽 포인터보다 앞에 있으면
# 왼쪽 포인터와 오른쪽 포인터의 값을 교환한다.
else
@array[left_pointer], @array[right_pointer] =
@array[right_pointer], @array[left_pointer]
# 다음 번 왼쪽 포인터와 오른쪽 포인터의 이동을 위해
# 왼쪽 포인터를 오른쪽으로 옮긴다.
left_pointer += 1
end
end
# 분할의 마지막 단계로 왼쪽 포인터의 값과 피벗을 교환한다.
@array[left_pointer], @array[pivot_index] =
@array[pivot_index], @array[left_pointer]
# 이어지는 예제에 나올 quicksort 메서드를 위해 left_pointer를 반환한다.
return left_pointer
end
end
퀵 정렬
퀵 정렬 알고리즘은 분할과 재귀로 이뤄진다. 알고리즘은 다음과 같이 동작한다.
- 배열을 분할한다. 피벗은 이제 올바른 위치에 있다.
- 피벗의 왼쪽과 오른쪽에 있는 하위 배열을 각각 또 다른 배열로 보고 1단계와 2단계를 재귀적으로 반복한다. (= 각 하위 배열을 분할하고 각 하위 배열에 있는 피벗의 왼쪽과 오른쪽에서 더 작아진 하위 배열을 얻는다. 이어서 이러한 하위 배열을 다시 분할하는 과정을 반복한다.
- 하위 배열이 원소를 0개 또는 1개 포함하면 기저조건이므로 아무것도 하지 않는다.

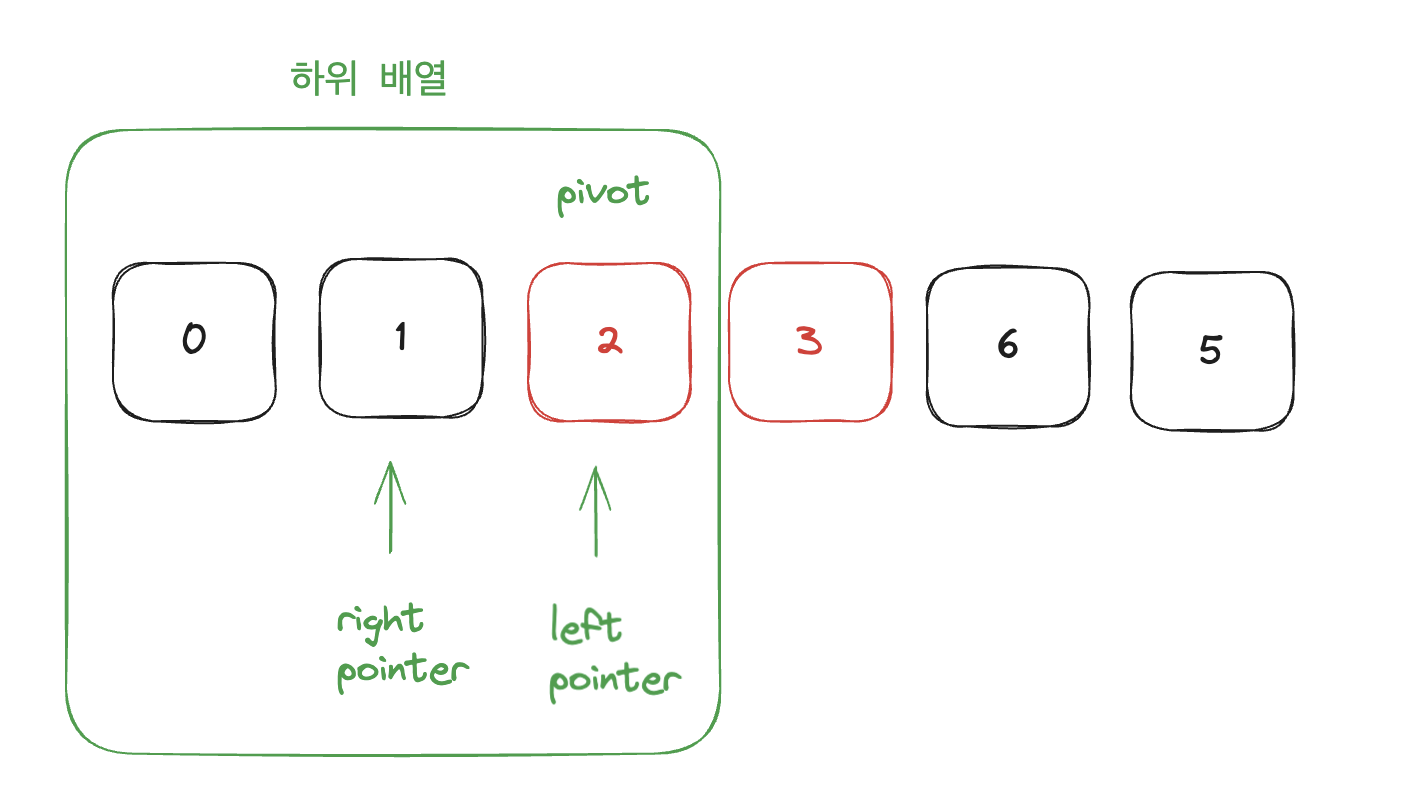


이후 다음 하위 배열은 0 하나만 들어있게 되고, 원소가 0개 또는 1개인 배열은 기저조건이므로 아무것도 하지 않는다.
이 배열은 자동으로 올바를 위치게 있다고 간주된다.
오른쪽의 하위 배열([6, 5])도 이와 같은 과정을 거쳐 정렬되게 한다.


코드 구현: 퀵 정렬
퀵 정렬을 성공적으로 끝내려면 다음 quicksort! 메서드를 앞서 보인 SortableArray 클래스에 추가한다.
def quicksort!(left_index, right_index)
# 기저 조건: 하위 배열에 원소가 0개 또는 1개일 때
if right_index - left_index <= 0
return
end
# 범위 내 원소들을 분할하고 피벗의 인덱스를 가져온다
pivot_index = partition!(left_index, right_index)
# 피벗 왼쪽에 대해 quicksort! 메서드를 재귀적으로 호출한다.
quicksort!(left_index, pivot_index - 1)
# 피벗 오른쪽에 대해 quicksort! 메서드를 재귀적으로 호출한다.
quicksort!(pivot_index + 1, right_index)
end다음과 같은 코드로 퀵 정렬 구현을 테스트해 볼 수 있다.
array = [0, 5, 2, 1, 6, 3]
sortable_array = SortableArray.new(array)
sortable_array.quicksort!(0, array.length - 1)
p sortable_array.array
퀵 정렬의 효율성
퀵 정렬의 효율성을 알아내려면 한 번 분할할 때의 효율성을 밝혀야 한다.
분할에 필요한 단계는 두 종류이다.
- 비교: 각 값과 피벗을 교환한다.
- 교환: 적절한 때에 왼쪽과 오른쪽 포인터가 가리키고 있는 값을 교환한다.
배열 내 각 원소를 피벗과 비교하므로 최소 N번 비교한다. (왼쪽과 오른쪽 포인터가 만날 때 까지 매 셀을 이동하기 때문이다)
하지만 교환 횟수는 정렬 여부에 따라 다르다.
모든 값을 교환한다고 하면 최대 N / 2 번 교환한다.
무작위로 정렬되어있는 데이터는 평균적으로 N / 4 번 정도 교환한다.
따라서 평균적으로 N번 비교하고 N / 4 번 정도 교환해서 대략 1.25N 단계가 걸린다.
빅오 표기법으로는 상수를 무시하므로 O(N) 시간에 분할을 진행한다고 볼 수 있다.
이는 한 번 분할할 때의 효율성이므로, 퀵 정렬의 효율성을 알기 위해서는 좀 더 분석해야 한다.
| N | logN | N x logN | 퀵 정렬 단계 수 (근사치) |
| 4 | 2 | 8 | 8 |
| 8 | 3 | 24 | 24 |
| 16 | 4 | 64 | 64 |
| 32 | 5 | 160 | 160 |
배열에서 원소가 8개일 때 퀵 정렬에 약 21단계가 걸린다.
- 8개 -> (왼쪽 하위 배열 정렬) 3개 -> 1개 -> 1개 -> (오른쪽 하위 배열 정렬) 4개 -> 2개 -> 1개 -> 1개
그러나 위의 표에서는 계산하기 쉽게 하기 위해 24 단계로 작성했다.
퀵 정렬은 O(NlogN) 알고리즘이다.

퀵 정렬의 최악의 시나리오
많은 알고리즘에서 최선의 경우는 배열이 이미 정렬됐을 때였다.
하지만 퀵 정렬에서 최선의 시나리오는 분할 수 피벗이 하위 배열의 한가운데 있을 떄다.
퀵 정렬의 최악의 시나리오는 배열이 오름차순 혹은 내림차순일 때, 피벗이 항상 배열의 한쪽 끝에 있을 때다.
최악의 시나리오에서는 8 +7 + 6 + 5 + 4 + 3 + 2 + 1 개의 원소를 분할하고,
이는 원소가 N개일 때 N + (N-1) + (N-2) ... + 1 단계가 걸리고, 이 공식은 N^2 / 2 로 표현될 수 있다.
따라서 최악의 시나리오에서 퀵 정렬의 효율성은 O(N^2) 이다.
퀵 정렬 vs 삽입 정렬
| 최선의 경우 | 평균적인 경우 | 최악의 경우 | |
| 삽입 정렬 | O(N) | O(N^2) | O(N^2) |
| 퀵 정렬 | O(NlogN) | O(NlogN) | O(N^2) |
평균적인 상황일 경우가 많으므로, 많은 언어에서 퀵 정렬을 사용하여 내장 정렬 함수를 구현하는 경우가 많다.
따라서 퀵 정렬을 직접 구현할 일은 거의 없다.
하지만 퀵 셀렉트라 불리는 매우 유사한 알고리즘이 실용적으로 쓸모가 있을 수 있다.
퀵 셀렉트
무작위로 정렬 된 배열이 있을 때, 정렬은 안해도 되지만 몇번째로 큰 값을 알고싶다고 하자.
ex) 시험 점수 백분위수, 중간 점수
퀵 정렬을 이용해 배열 내 모든 값들을 정렬한 다음에 구해도 되지만 O(NlogN)의 시간 복잡도가 걸리므로,
이러한 경우에는 퀵셀렉트(Quickselect) 알고리즘으로 훨씬 더 나은 성능을 낼 수 있다.
퀵 셀렉트도 분할에 기반하며, 퀵 정렬과 이진 검색의 하이브리드 정도로 생각할 수 있다.
퀵 셀렉트는 분할을 진행하며 피벗이 정렬이 되었을 때, 피벗의 인덱스 위치를 알 수 있다.
다른 값들은 정렬되어있지 않아 알 수 없지만, 유일하게 정렬된 피벗은 몇번째로 큰 수인지 알 수 있다.
정렬된 피벗이 다섯번째 값이고, 두번째로 큰 값을 찾는다고 하자.
그렇다면 피벗보다 작은 값(왼쪽 요소들)의 하위 배열을 만들어 탐색을 진행하면 된다.
또, 피벗보다 큰 값(오른쪽 요소들)은 계산할 필요가 없어지므로 시간을 절약할 수 있다.
퀵 셀렉트의 효율성
퀵 셀렉트의 효율성은 예상했던 O(logN)이 아닌, O(N)이다.
원소가 8개인 배열에서 3번 분할하는데, 8 + 4 + 2 = 대략 14 단계가 걸린다.
이는 공식으로 표현하면 N + (N/2) + (N/4) ... + 2 단계다. 합하면 항상 약 2N 단계가 걸린다.
빅 오는 상수를 무시하므로 퀵 셀렉트의 효율성은 O(N)이다.
코드 구현: 퀵 셀렉트
def quickselect!(kth_lowest_value, left_index, right_index)
# 기저 조건이면, 즉 하위 배열에 셀이 하나면 찾고 있던 값을 찾은 것이다.
if right_index - left_index <= 0
return @array[left_index]
end
# 배열을 분할하고 피벗의 위치를 가져온다.
pivot_index = partition!(left_index, right_index)
# 찾고 있는 값이 피벗 왼쪽에 있으면
if kth_lowest_value < pivot_index
# 피벗이 왼쪽의 하위 배열에 대해
# 재귀적으로 퀵 셀렉트를 수행한다.
quickselect!(kth_lowest_value, left_index, pivot_index - 1)
# 찾고 있는 값이 피벗 오른쪽에 있으면
elsif kth_lowest_value > pivot_index
# 피벗 오른쪽의 하위 배열에 대해
# 재귀적으로 퀵 셀렉트를 수행한다.
quickselect!(kth_lowest_value, left_index + 1, pivot_index)
else # kth_lowest_value == pivot_index
# 분할 후 피벗의 인덱스가 k번째 작은 값의 인덱스와 같으면
return @array[pivot_index]
end
end
정렬되지 않은 배열에서 두 번쨰로 작은 값을 찾고 싶다면 다음 코드를 실행한다.
array = [0, 50, 20, 10, 60, 30]
sortable_array = SortableArray.new(array)
p sortable_array.quickselect!(1, 0, array.length - 1)quickselect! 메서드는 첫 번째 인수에 0부터 시작하는 인덱스 위치를 받는다.
두 번째로 작은 값을 원하면 1을 넘긴다.
두 번째 인수와 세 번째 인수는 각각 배열의 왼쪽 인덱스와 오른쪽 인덱스다.
다른 알고리즘의 핵심 역할을 하는 정렬
퀵 정렬 외에도 병합 정렬(Mergesort) 역시 재귀를 사용한 잘 알려진 O(NlogN) 정렬 알고리즘이다.
여기서 중요한 점은 가장 빠른 정렬 알고리즘이 O(NlogN)이라는 사실인데, 이 속도가 다른 알고리즘에도 영향을 미치기 때문이다.
정렬되지 않은 배열이 있고, 그 배열 중에 중복값이 있는지 확인하는 문제가 있다고 하자.
(메모리를 더 사용해서 O(N)으로 풀 수 있는 알고리즘은 제외한다. - 19장에서 다룰 예정)
4장에서 이 문제는 효율성이 O(N^2) 이었다.
정렬을 먼저 진행하고, 루프를 돌아 매 숫자를 검사하며 그 다음 숫자와 동일한지 확인하면 된다.
원래 배열이 [5, 9, 3, 2, 4, 5, 6]이었다고 한다면 정렬된 배열은 [2, 3, 4, 5, 5, 6, 9]가 된다.
// 자바 스크립트
function hasDulicateValue(array) {
// 먼저 배열을 정렬한다.
// (자바스크립트에서 숫자를 "알파벳"순이 아닌 크기순으로 정렬하려면
// 정렬 함수를 다음과 같이 사용해야한다.)
array.sort((a, b) => (a > b) ? -1 : 1);
// 배열의 각 값을 마지막 값까지 순회한다.
for(let i = 0; i < array.length - 1; i++) {
// 현재 값이 배열의 가음 값과 같으면
// 중복을 찾은 것이다.
if (array[i] == array[i+1]) {
return true;
}
}
// true를 반환하지 않고 배열 끝까지 왔으면
// 중복이 없다는 뜻이다.
return false;
}이때의 알고리즘은 O(NlogN) + N 단계가 걸리게 된다.
빅 오는 높은 차수의 N만 남기므로 O(N^2)에서 O(NlogN)인 알고리즘으로 개선할 수 있게 되었다.
마무리
퀵 정렬과 퀵 셀렉트라는 효율적인 해결법을 제시하는 재귀 알고리즘을 배우게 되었다.
보다 고급 알고리즘을 배웠으니 다음은 재귀를 사용해 연산하는 자료 구조를 완벽히 다룰 준비가 됐다.
다음 장에서는 다양한 애플리케이션에 힘이 되는 자료 구조의 특별한 능력에 대해 알아 볼 것이다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [책] 누구나 자료구조와 알고리즘 - 14장 노드 기반 자료 구조 (0) | 2024.01.15 |
|---|---|
| [책] 누구나 자료구조와 알고리즘 - 17장 트라이(trie)해 보는 것도 나쁘지 않다 (1) | 2024.01.01 |
| [책] 누구나 자료구조와 알고리즘 - 11장 재귀적으로 작성하는 법 (0) | 2023.12.12 |
| [책] 누구나 자료구조와 알고리즘 - 10장 재귀를 사용한 재귀적 반복 (0) | 2023.12.04 |
| [책] 누구나 자료구조와 알고리즘 - 9장 스택과 큐로 간결한 코드 생성 (0) | 2023.12.04 |



